Testing for the Data Scientist

Data collection, modeling, and analysis. These are tasks that the modern data scientist is expected to perform with statistical precision and ethical decision making. The code we write is not for accomplishing tasks that are easily verifyable like, "As a user, I want to login to my account using GitHub." As data science begins to mature, more and more articles are being written about ensuring proper behavior for complex machine learning systems.

As I delve into data science more myself, I am surprised at the unfortunate inattention paid to the lessons already learned by software engineers, particularly around testing and clean code. For those unfamiliar with tests, I simply mean automated methods that verify behavior in a given piece of software–whether that be a calculator app or an AI-based intrusion detection system.

Think about this. Data scientists, ML engineers, and data engineers are expected to often write more logically difficult code than the average developer and yet rarely spend time writing tests to ensure proper behavior. It simply doesn't make sense. As Edmund Burke famously said, "Those who don't know history are doomed to repeat it."

Lightning Introduction to Unit Testing

(Feel free to skip to the next section if you're already familiar with unit testing.)

What are unit tests? These are automated tests that focus on ensuring proper behavior for a given set of functions or methods within a given context such as an OOP class. Generally speaking, each test assertion is a simple, easy-to-read description of a function's output given a particular input. Here's a ridiculously simple test in Python of an add function:

# In calculator.py
def add(x, y):
    return x + y

# In calculator_test.py
from calculator import add

def test_addition():
    assert add(1, 2) == 3

❯ pytest calculator_test.py
============================= test session starts ==============================

calculator_test.py .                                                     [100%]

=========================== 1 passed in 0.01 seconds ===========================

Case Study: A Tensorflow Loss Function

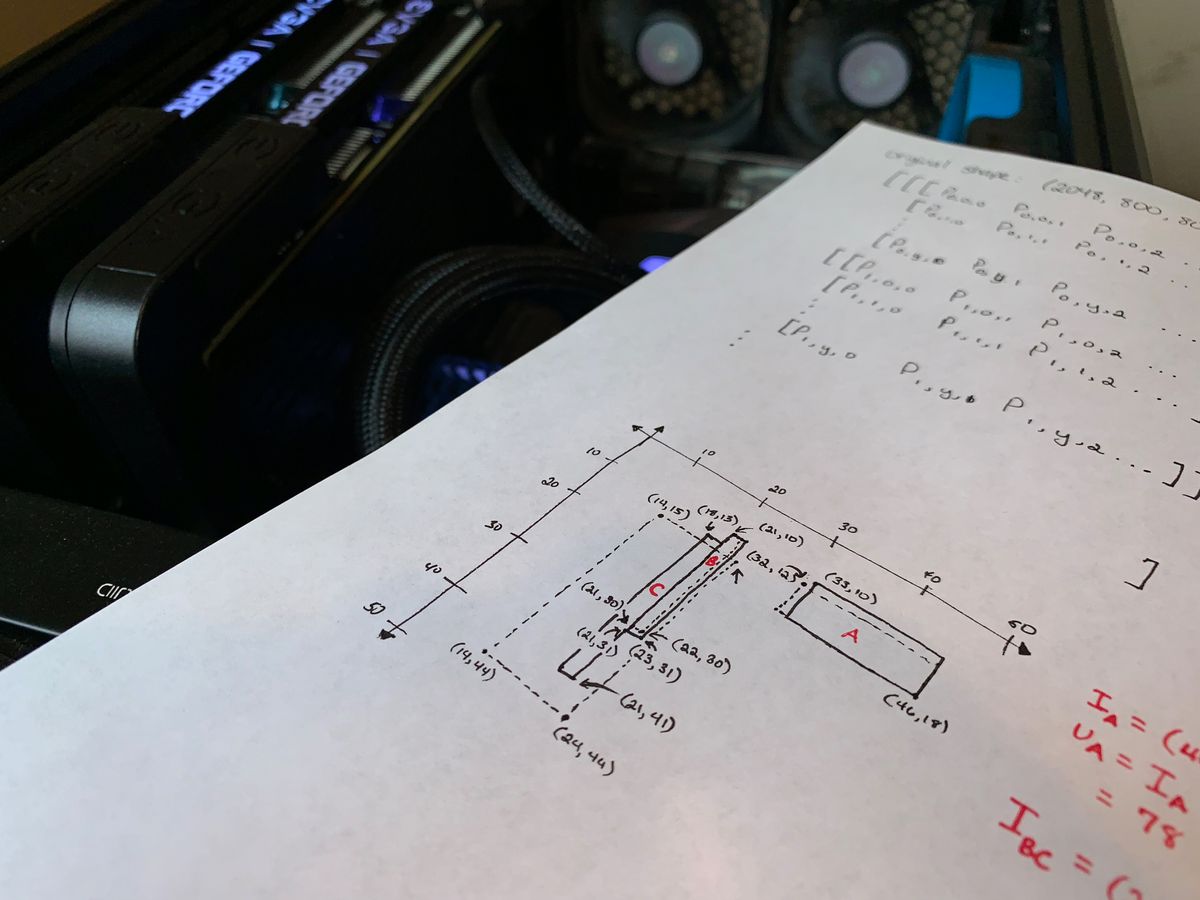
Those involved in Deep Learning and more specifically Tensorflow will know that building up computational graphs is not terribly easy. Providing a differentiable loss function for backpropogation can sometimes require direct calls to the Tensorflow API. I recently had to write an intersection-over-union (IoU) function that compared a set of predicted versus actual bounding boxes as opposed to the built-in mean_iou function that compares bounding boxes row-by-row. Here's an example of the algorithm using three sample bounding boxes:

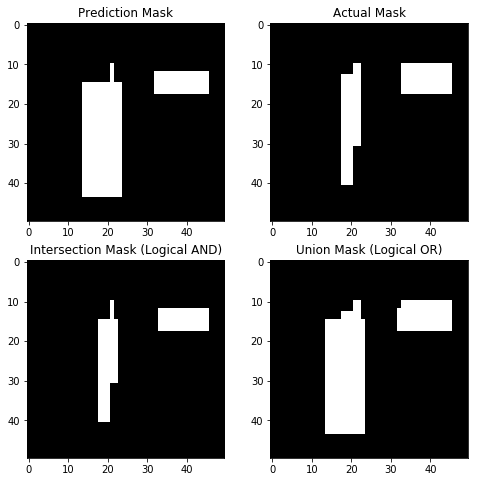
Apparently, this type of loss function is far from standard. Because this determines the entire process of training, it was essential for the calculations to be accurate. To this end, I did some calculations by hand to make sure I got an expected result (as seen in the poster image). Therefore, the goal of the automated test is this:

Write a test that passes both predictions and actual values to the loss function and returns a tensor that evaluates to the proper IoU score.

To maintain proper isolation of testing a single loss function "unit," I take advantage of pytest's fixture syntax to have a sample of predicted and actual values for a single batch:

# In conftest.py
import pytest
import numpy as np

@pytest.fixture
def sample_pred():
    return np.array([
        # x1, y1, x2, y2, prob
        [[ 32,  12,  46,  18, 0.7],
         [ 21,  10,  22,  30, 0.8],
         [100, 100, 100, 100, 0.2],
         [ 14,  15,  24,  44, 0.1],
         [200, 200, 200, 200, 0.2]]
    ], dtype=np.float32)

@pytest.fixture
def sample_actual():
    return np.array([
        # x1, y1, x2, y2, prob
        [[33, 10, 46, 18, 0.8],
         [21, 10, 23, 31, 0.3],
         [ 0,  0,  0,  0, 0.0],
         [18, 13, 21, 41, 0.2],
         [ 0,  0,  0,  0, 0.0]]
    ], dtype=np.float32)

Unfortunately, the test cannot simply call the function like the calculator example. Loss functions with Tensorflow describe the GPU-operation but don't actually run them. In other words, the return value of this spatial_iou function is actually a Tensor, not a numerical result. Thankfully, Tensorflow has an tf.InteractiveSession that allows explicit evaluation of a Tensor with given inputs.

# In loss_test.py
def test_spatial_iou(sample_pred, sample_actual):
    sess = tf.InteractiveSession()

    # Mix up inputs (shouldn't be index dependent)
    pred_t = tf.constant(sample_pred[:, [0, 1, 3], :])
    actual_t = tf.constant(sample_actual[:, [1, 3, 0], :])

    # Pass image shape and tensors to loss function
    tensor = spatial_iou((50, 50), actual_t, pred_t)

    # Initialize `tf.Variable`s
    tf.global_variables_initializer().run()

    # Explicitly evaluate using the tf.InteractiveSession
    result = tensor.eval()

    # Result calculated by hand
    assert result == approx(0.463942308, abs=0.00001)

    # Close the interactive session
    sess.close()

As seen in the comments, the test requires a little bit of setup. However, with this test written, I can now freely write the implementation with the confidence that I have a secondary check on my logic. Additionally, I now have an automated check in case a new Tensorflow API change necessitates changing my implementation or another programmer wants to understand the purpose of this loss function.

For reference, here is the final implementation:

import tensorflow as tf
import keras.backend as K
from toolz.curried import curry

def spatial_iou(image_shape, actual, pred):
    @tf.contrib.eager.defun
    def _spatial_iou(tensor):
        actual, pred = tensor

        pred_empty_canvas = tf.Variable(lambda: tf.zeros(image_shape))
        actual_empty_canvas = tf.Variable(lambda: tf.zeros(image_shape))

        pred_masks = tf.equal(tf.map_fn(mask_true(pred_empty_canvas), tf.round(pred)), 1)
        pred_canvas = tf.reduce_any(pred_masks, axis=0)

        actual_masks = tf.equal(tf.map_fn(mask_true(actual_empty_canvas), tf.round(actual)), 1)
        actual_canvas = tf.reduce_any(actual_masks, axis=0)

        intersection_mask = tf.logical_and(pred_canvas, actual_canvas)
        union_mask = tf.logical_or(pred_canvas, actual_canvas)

        intersection = tf.reduce_sum(tf.cast(intersection_mask, tf.float32), name='intersection')
        union = tf.reduce_sum(tf.cast(union_mask, tf.float32), name='union')

        return intersection / union

    iou = tf.map_fn(_spatial_iou, (actual, pred), dtype=tf.float32)

    return K.mean(iou)

@curry
def mask_true(canvas, t):
    x1 = tf.to_int32(t[0])
    y1 = tf.to_int32(t[1])
    x2 = tf.to_int32(t[2])
    y2 = tf.to_int32(t[3])

    shape = tf.shape(canvas)
    x_start = tf.maximum(0, x1)
    y_start = tf.maximum(0, y1)

    x_delta = tf.cond(tf_cond_all([
        tf.greater_equal(x1, 0),
        tf.greater_equal(x2, x1),
        tf.less_equal(x1, shape[1]),
        tf.less_equal(x2, shape[1])
    ]), lambda: x2 - x1, lambda: tf.constant(0))

    y_delta = tf.cond(tf_cond_all([
        tf.greater_equal(y1, 0),
        tf.greater_equal(y2, y1),
        tf.less_equal(y1, shape[0]),
        tf.less_equal(y2, shape[0])
    ]), lambda: y2 - y1, lambda: tf.constant(0))

    area = tf.ones((y_delta, x_delta))

    return canvas[y_start:(y_start + y_delta),
                  x_start:(x_start + x_delta)].assign(area)

For more details on how to write Python tests, check out the pytest documentation.

Discussion

Writing tests is not a natural discipline; it is not an innate desire. Most coding bootcamps barely cover it if at all–data science programs even less. While it is important to understand algorithms and statistics for data science, our goal as data scientists is to accurately and confidently use data to assist fellow humans. Having rigorous practices that provide concrete steps to achieving this goal ought to be embraced.

The primary purpose of testing is to increase confidence and maintainability. It doesn't mean mandatory 100% test coverage. Some systems are more difficult to test than others. Using statistics for model accuracy is a perfect example. Proper metrics give greater confidence that the model will perform as expected. Likewise, unit tests where possible increase our confidence that we don't have bugs that artificially inflate assurance in a given model or analysis.

Do yourself a favor--write tests and don't assume you can remember everything.

Links & References

Venners, B. (2002). Test-driven development. Retrieved on Dec 17, 2018, from https://www.artima.com/intv/testdrivenP.html